L'Ange contre le Démon

Salut salut, c'est la première fois que je fais un article de maths, j'espère que ça vous plaira ! Bien évidemment, je ne rentrerai pas dans les détails et ce sera, pour la plupart des preuves, un truc du style "On voit bien que ça marche.".

Introduction

Aujourd'hui, je vais vous parler du problème assez connu appelé jeu de l'ange et du démon. C'est un problème posé en 1996 par John Conway dans un article scientifique. Pour info, Conway est connu notamment pour son jeu de la vie, même s'il n'aimait pas qu'on se souvienne de lui que pour ça, parce qu'il a fait beaucoup d'autres découvertes d'un niveau plus élevé.

Les règles du jeu

Le jeu se joue sur un plateau de taille infini, avec des cases carrées, et 2 joueurs s'affrontent : un ange et un démon. Le but du démon est d'enfermer l'ange, et le but de l'ange est de réussir à toujours s'échapper. Les deux joueurs jouent chacun leur tour.

• Lorsque le démon joue, il peut brûler une case qui n'est pas encore brûlée (au début, aucune case n'est brûlée)
• Lorsque l'ange joue, il peut se déplacer à une case à une distance (pour la norme infinie dans ${\mathbb{Z}}^2$) maximale de 3 qui n'est pas brûlée (et l'ange a des ailes donc il peut par exemple "sauter" par dessus une "barrière" brûlée qui ferait 1 case d'épaisseur)

Le jeu étant déterministe, un des deux joueurs possède une stratégie gagnante. La question est : existe-t-il un algorithme qui permette au démon d'enfermer l'ange ?

Si on voulait vraiment définir "enfermer" rigoureusement, j'imagine qu'on pourrait dire que cela correspond au moment où l'ensemble des cases atteignables en autant de coups d'ange qu'on veut est fini, ou au moment où l'ange est coincé sur une seule case, en fait les deux versions sont trivialement équivalentes.

En rouge, la position de l'ange, en noir, les cases brûlées, en vert les cases où l'ange peut aller.

Un peu de recul

Je vous ai décrit plus haut le cas de l'ange de puissance 3 (i.e : qui peut se déplacer de 3 cases). Il est évident que si n < m et que l'ange de puissance n peut s'échapper, alors l'ange de puissance m peut s'échapper. Il doit donc exister r $\in \bar{\mathbb{N}}$ (éventuellement égal à $+\infty$) tel que le démon a une stratégie gagnante pour enfermer l'ange si et seulement si la puissance de l'ange est strictement inférieur à r.

Spoiler alert : En 2006, quatre travaux indépendants ont prouvé que r était égal à 2. Je vais utiliser à ma sauce les preuves de Mathé, dont je n'ai pas rapidement trouvé de lien vers sa publication gratuitement, et Kloster.

Ce qu'on va prouver

Je ne vais pas prouver que l'ange de puissance 1 perd contre un démon qui joue parfaitement. Nous allons seulement "prouver" qu'il existe une stratégie gagnante pour l'ange de puissance 2.

L'ange intelligent ("idée de moi")

On appelle case anciennement accessible une case c pour laquelle il existe un tour t strictement inférieur au [tour actuel - 1] tel que c_t est à une distance inférieure à la puissance de l'ange pour la norme infinie. En gros, c'est une case sur laquelle l'ange a, à un moment, été à 1 coup de pouvoir y aller.

On appelle "ange intelligent" un ange qui ne passe jamais par une case "anciennement accessible".

On va montrer que :

Un démon a une stratégie gagnante contre les anges intelligents <=> Un démon a une stratégie gagnante contre les anges

L'implication indirecte est évidente. Montrons l'implication directe.

Supposons qu'un démon aie une stratégie S1 gagnante contre les anges intelligents.

Soit S2 définit de cette manière :

Soit c la suite des cases parcourues par l'ange.

- Si c est intelligent (i.e : $\forall (i,j)tq|i-j|\ge 2,\Vert {\mathbf{c}}_{\mathbf{j}}\mathbf{-}{\mathbf{c}}_{\mathbf{i}}{\Vert }_2>2$), alors on renvoie la réponse de S1.

- Sinon, alors on note c' qui est c auquel on a retiré les "passages non intelligents" (si de tels i et j existent avec i < j, alors l'élément qui suit c_i dans la suite c' est c_j et on saute les éléments entre i et j dans c).
- Si S2(c') est brûlé, on ne renvoie rien.
- Sinon, on renvoie S2(c').

Si c est intelligent, S2 brûle les mêmes cases que S1 donc S2 gagne. Sinon, "c'" est un jeu possible auquel S2 gagne. En fait, jouer S2(c) revient à jouer S2(c') auquel on a ajouté quelques cases brûlées, donc le démon gagne aussi en jouant S2(c). Donc le démon a une stratégie gagnante contre les anges.

Il y a volontairement une ambiguïté entre la suite c', la suite finie c' qui s'arrête à l'élément n et l'élément c'_n. Mais je raccourcis la démonstration, vous comprenez l'idée.

Le démon gentil (idée de Mathé)

Le démon gentil ("nice devil") est semblable au démon, à l'exception qu'il se force à ne jamais brûler une case anciennement accessible, et qu'il a le droit de ne rien faire à un tour.

Montrons que :

Le démon a une stratégie gagnante <=> Le démon gentil a une stratégie gagnante

L'implication indirecte est évidente. Montrons l'implication directe.

Supposons que le démon aie une stratégie gagnante. On va montrer que le démon gentil en a une.

Le démon a une stratégie gagnante contre les anges intelligents, qu'on note S. On définit S' qui est :

- Si S renvoie une case anciennement accessible, on ne renvoie rien.

- Sinon, on renvoie la réponse de S.

Soit un ange intelligent. Supposons par l'absurde qu'il puisse échapper à S'. En jouant de la même manière contre S qu'il a joué contre S', il pourrait échapper à S. En effet, tous ses coups restent légaux car les différences de cases brûlées entre les 2 parties se jouent à des cases anciennement accessibles, qui n'apparaissent donc pas dans le chemin de l'ange puisqu'il est intelligent. C'est absurde car S est une stratégie gagnante contre les anges intelligents.

Donc l'ange intelligent ne peut pas échapper à S'. Donc S' est une stratégie gagnante pour le démon gentil.

L'éclaireur (idée de Kloster)

On va maintenant prendre un algorithme gagnant pour l'ange (de puissance 2) qui doit affronter un démon gentil. On va juste modifier les conditions de victoire pour simplifier : le démon gentil gagne s'il fait reboucler l'ange sur une case où il est déjà passé, et dans le même sens (ce nouveau jeu est bien équivalent parce que lorsque l'ange a un nombre fini de cases accessibles en plusieurs coups, il reboucle sur lui-même, et par un argument similaire à ce qui a été fait précédemment, l'ange ne veut pas reboucler sur lui-même dans le même sens car ça veut dire qu'il est collé au même mur et entre temps le démon gentil a simplement rajouté des murs).

On va représenter les cases brûlées par des murs en forme d'octogones (pour représenter le fait de pouvoir passer "en diagonale" plus facilement).

L'ange qui joue avec cette stratégie sera appelé l'éclaireur.

La stratégie est la suivante : Il imagine que toutes les cases d'abscisse strictement négative sont des murs. L'éclaireur va le plus loin possible qui pourrait être un coup légal d'un ange en longeant le mur (et en restant collé au mur) et en essayant de tourner dans le sens horaire autour de l'octogone représentant le mur (si le mur est à gauche de l'éclaireur, l'éclaireur monte. S'il est en haut, il va à droite. S'il est à droite, il descend...).

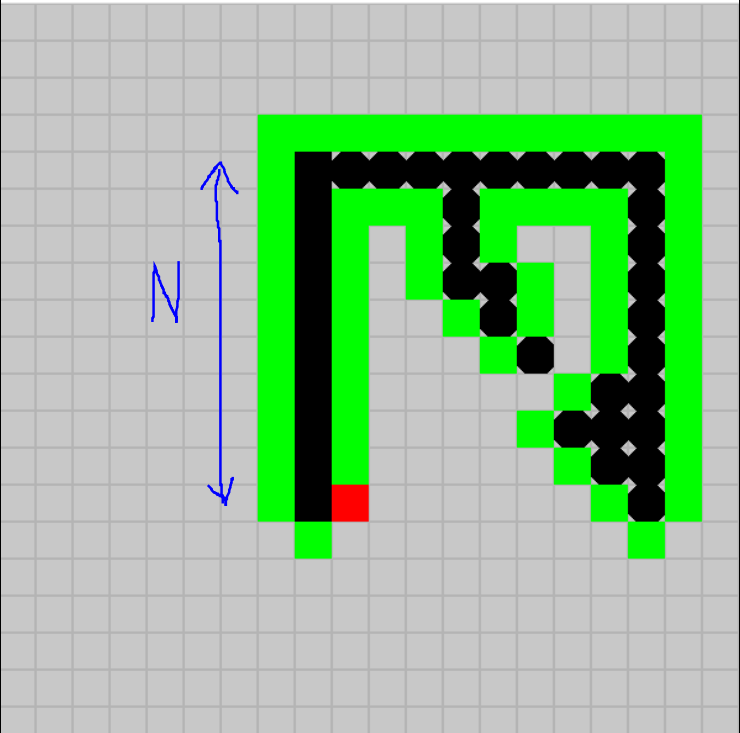
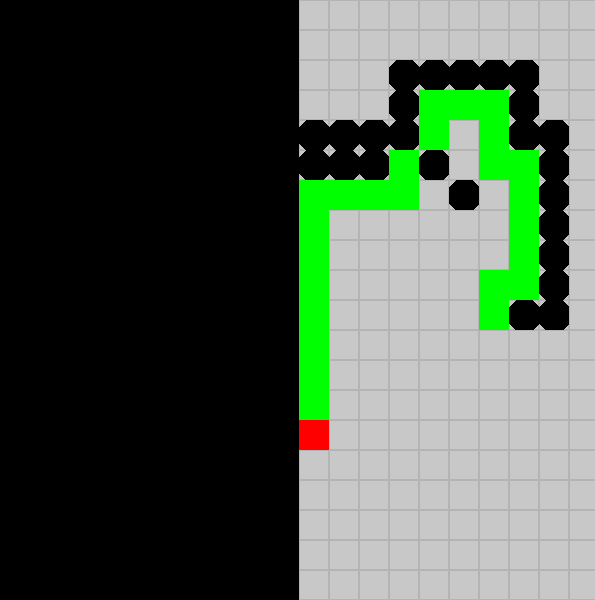En rouge, le point de départ. En vert, le chemin parcouru.

Preuve de la réussite de cet algorithme

Supposons par l'absurde que le démon gentil gagne. Notre ange doit avoir fait une boucle, et aussi doit repartir dans le même sens.

PS : J'ai pas envie de refaire ma remarque sur le fait qu'un ange qui reboucle sur lui-même est pas "optimal" mais y'aurait des trucs à dire.

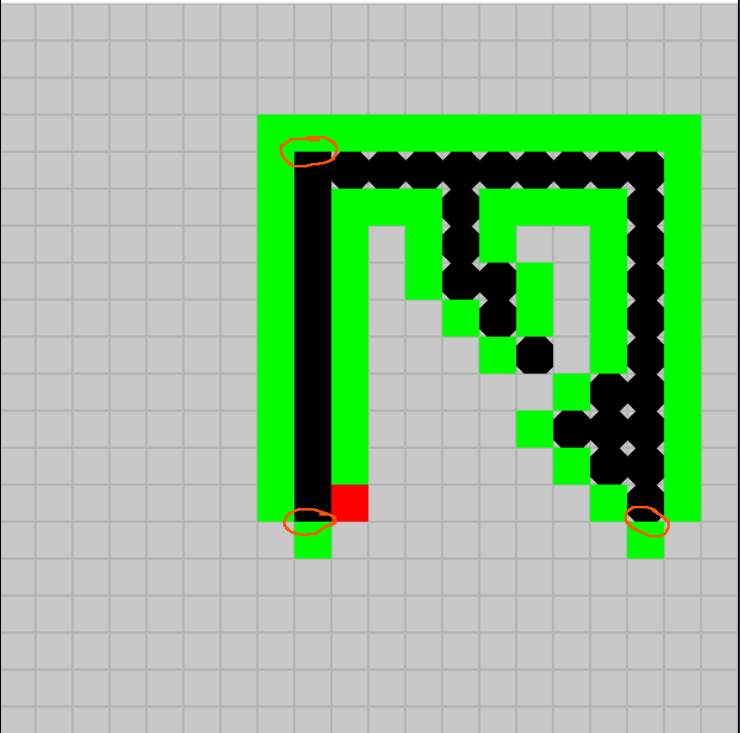
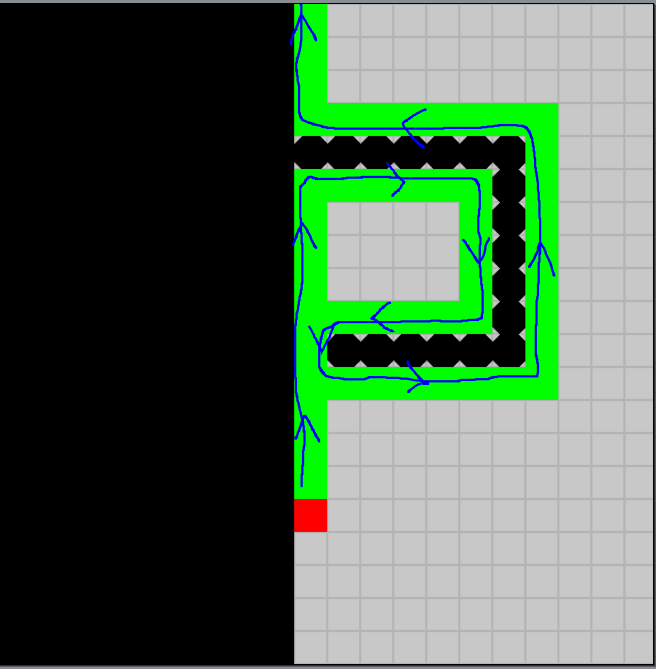Ici, l'ange n'est pas enfermé, même s'il est passé 2 fois par la même case.

La seule manière pour le démon gentil qui ne peut pas recouper le "fil vert" de faire faire une boucle à l'ange, c'est de le faire recouper sur son point d'origine.

Si vous êtes pas convaincus, regardez l'image au-dessus, et j'ai pas réussi à le prouver d'une autre manière que "ça se voit". Je pense que la preuve se ferait bien en distinguant les cas "on reboucle sur un chemin qui monte en arrivant de la droite"... et en fait les cas "on reboucle sur un chemin qui * en arrivant de *" sont pour beaucoup symmétriques je pense.

Le coeur de la preuve (idée de Kloster)

Supposons que le démon gentil aie réussi à faire boucler sur le chemin initial.

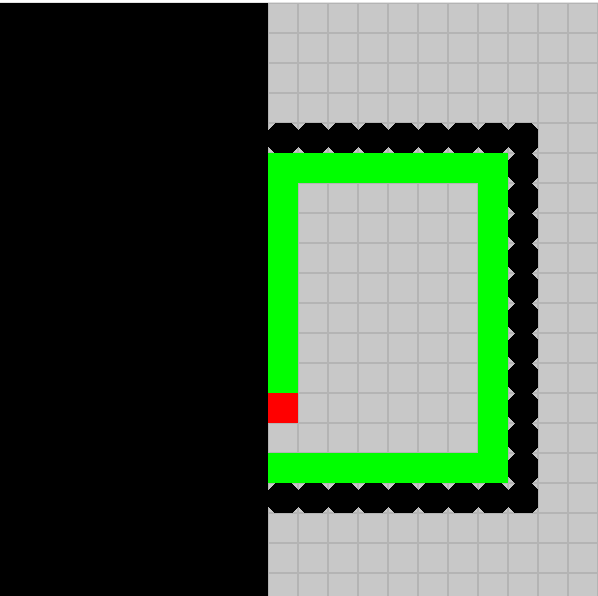
Je vais faire des trucs bizarres, mais on essaie juste de construire une contradiction.

Nous allons mettre en pause une partie gagnante pour le démon gentil au tour t au moment où l'ange s'apprête à sauter sur une case avec une ordonnée strictement négative (ce moment existe car le "mur" qui encercle passe en-dessous du départ, oui la rigueur commence à disparaître on arrive à la fin de l'article, mais accrochez-vous !!). Par ailleurs, on a potentiellement arrêté le temps au milieu d'un tour (si l'ange était en y=1 et se déplaçait en y=-1).

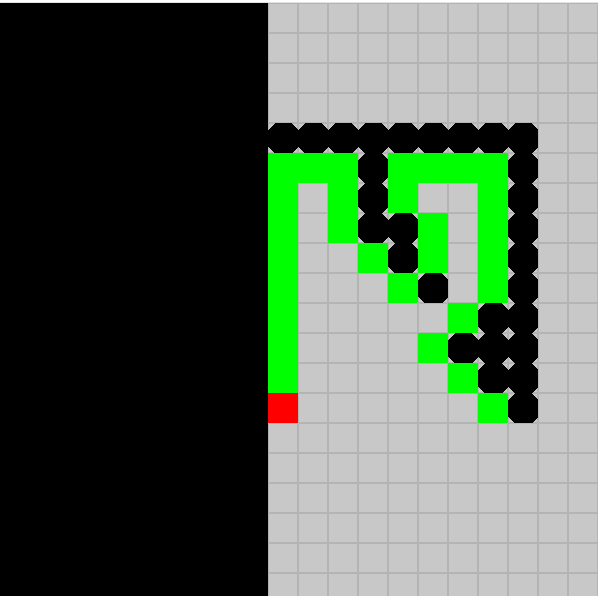
On va enlever notre barrière imaginaire et brûler à gauche une ligne d'abscisse x=-1 entre y=0 et l'ordonnée maximale des murs construits par le démon gentil. Cette ligne sera de taille N (N cases brûlées). De plus, on va laisser l'ange terminer sa course (à noter que ce n'est pas la suite du jeu, ce n'est même pas la boucle que le démon commptait lui faire prendre) et rejoindre son point de départ.

Nous allons maintenant procéder à des comptages

Comptage numéro 1

On note s le nombre de cases brûlées. Le démon gentil ne pouvant brûler qu'au plus 1 case par tour, il y a maintenant au plus N + t cases brûlées.

$s\le N+t$ [0]

Comptage numéro 2

On va noter e (pour edges) le nombre de côtés d'une case brûlée qui sont adjacents à une case verte. On voit bien qu' à chaque tour de jeu, l'ange a "peint" (est passé à côté) au minimum 2 côtés de cases brûlées (sauf peut-être au tour t, qui est peut-être interrompu). On a donc :

$e\ge 2t-1pendantlaphasedejeu$

Rajoutons à cela 3 côtés spécifiques :

Rajoutons à cela les côtés peints par le retour par-dessus la barrière (au moins N qui sont face à droite pour remonter et 2 faces vers le haut pour retourner à gauche).

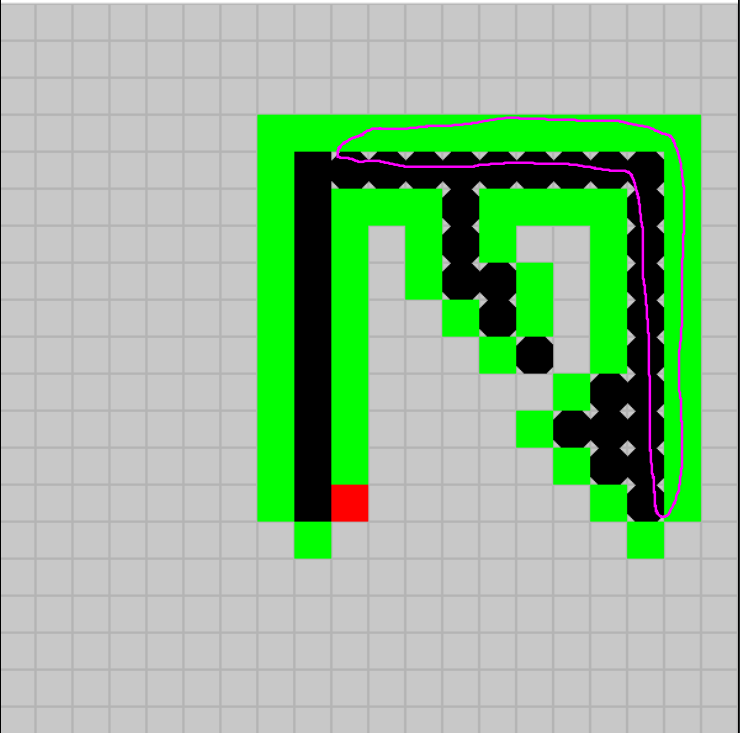
Rajoutons à cela les N faces côtés gauche peints sur le mur vertical à gauche.

On obtient :

$e\ge 2t+2N+4$ [1]

Comptage numéro 3

On a 4s "comptés avec leur ordre de multiplicité" côtés de carrés brûlés (j'en compte 8 même si 2 carrés brûlés sont côte-à-côte et se partagent un côté). Autrement dit, les p côtés partagés comptent double. Les côtés partagés ne pouvant pas être peints en verts, on a :

$4s\ge e+2p$ [2]

C'est pas un p pour "peint" mais pour "partagé".

De plus, par récurrence sur s, on a :

$p\le s-1$ [3]

Fin de la preuve

Insérez [1] et [3] dans [2] et on obtient :

$s\ge t+N+1$

Cela contredit [0], donc on conclue que le l'ange n'a pas rebouclé. Donc le démon gentil n'a pas de stratégie gagnante contre l'éclaireur. Donc il existe une stratégie gagnante pour l'ange de puissance 2 (celle de l'éclaireur n'en est pas une, elle ne fonctionne que contre le démon gentil !).

Pour aller plus loin

En fait, la preuve de Kloster est même plus forte que cela. Lorsqu'on suit la preuve, on se rend compte qu'elle reste valide pour un ange de ce type :

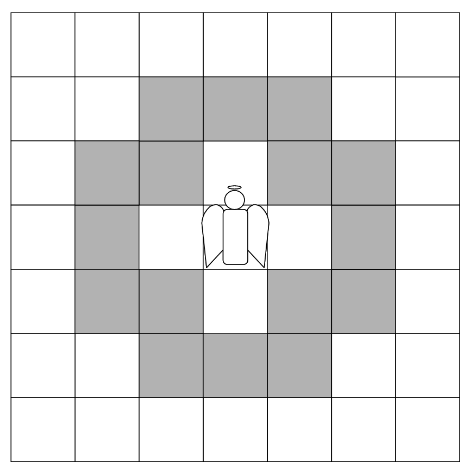
Aujourd'hui, voilà le plus petit ange que j'ai retrouvé qui pouvait s'échapper 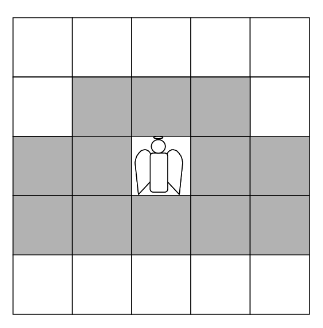et la source de l'article.

De ce que j'ai vu sur internet, on pense qu'un ange qui bougerait comme un cavalier est censé perdre, mais on ne l'a pas encore prouvé.

Conclusion

Merci d'avoir suivi jusqu'au bout ! J'espère que c'était clair, n'hésitez pas à me donner des retours.

Lucalgèbre